Van der Waerden Puzzle

In [1] a puzzle is mentioned:

Find a binary sequence \(x_1, \dots , x_8\) that has no three equally spaced \(0\)s and no three equally spaced \(1\)s

I.e. we want to forbid patterns like \(111\),\(1x1x1\), \(1xx1xx1\) and \(000\),\(0x0x0\), \(0xx0xx0\). It is solved as a SAT problem in [1], but we can also write this down as a MIP. Instead of just 0s and 1s we make it a bit more general: any color from a set \(c\) can be used (this allows us to use more colors than just two and we can make nice pictures of the results). A MIP formulation can look like the two-liner:

\[\begin{align}& x_{i,c} + x_{i+k,c} + x_{i+2k,c} \le 2 && \forall i,k,c  \text{ such that } i+2k \le n\\ & \sum_c x_{i,c}=1 && \forall i\end{align} \]

where \(x_{i,c} \in \{0,1\}\) indicating whether color \(c\) is selected for position \(i\). For \(n=8\) and two colors we find six solutions:

For \(n=9\) we can not find any solution. This is sometimes denoted as the Van der Waerden number \(W(3,3)=9\).

For small problems we can enumerate these by adding cuts and resolving. For slightly larger problems the solution pool technique in solvers like Cplex and Gurobi can help.

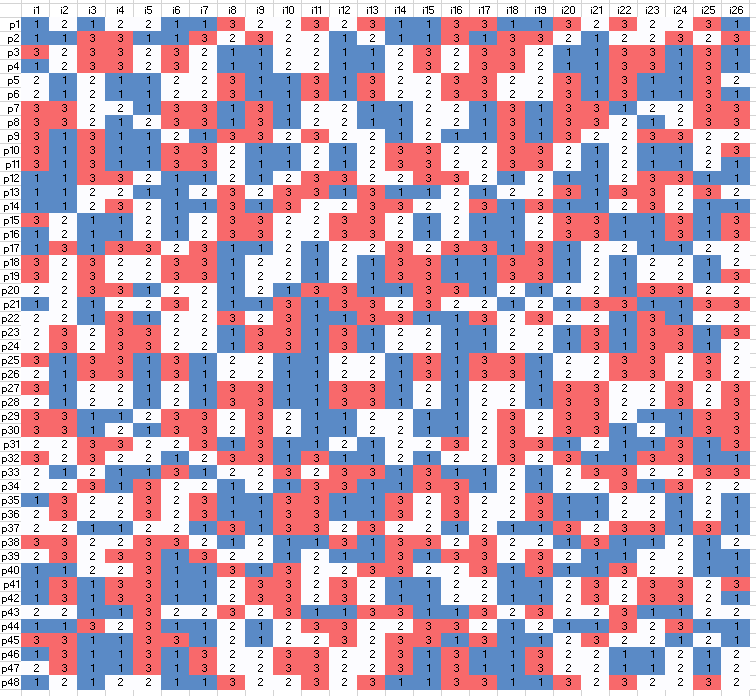
For three colors \(W(3,3,3)=27\) i.e. for \(n=27\) we cannot find a solution without three equally spaced colors. For \(n=26\) we can enumerate all 48 solutions:

Only making this problem a little bit bigger is bringing our model to a screeching halt. E.g. \(W(3,3,3,3)=76\). I could not find solutions for \(n=75\) within 1,000 seconds, let alone enumerating them all.

MIP vs CP formulation

In the MIP formulation we used a binary representation of the decision variables \(x_{i,c}\). If we would use a Constraint Programming solver (or an SMT Solver), we can can use integer variables \(x_i\) directly.

Binary MIP formulation	Integer CP formulation
\[\large{\begin{align}\min\>&0\\& x_{i,c} + x_{i+k,c} + x_{i+2k,c} \le 2 &&  \forall  i+2k \le n\>\forall c \\ & \sum_c x_{i,c}=1 && \forall i\\ & x_{i,c} \in \{0,1\} \end{align}} \]	\[ \large{\begin{align} &x_{i} \ne x_{i+k} \vee x_{i+k} \ne x_{i+2k} && \forall  i+2k \le n\\ & x_i \in \{1,\dots,nc\} \end{align} }\]

Python/Z3 version

This is to illustrate the integer CP formulation. Indexing in Python starts at 0 so we have to slightly adapt the model for this:

from z3 import *

n = 26
nc = 3

# integer variables X[i]
X = [ Int('x%s' % i ) for i in range(n) ]

# lower bounds X[i] >= 1
Xlo = And([X[i] >= 1 for i in range(n)])
# upper bounds X[i] <= nc
Xup = And([X[i] <= nc for i in range(n)])
# forbid equally spaced colors 
Xforbid = And( [ Or(X[i] != X[i+k+1], X[i+k+1] != X[i+2*(k+1)] ) for i in range(n) \
               for k in range(n) if i+2*(k+1) < n])
# combine all constraints
Cons = [Xlo,Xup,Xforbid]
       
# find all solutions    
s = Solver()
s.add(Cons)
k = 0
res = []
while s.check() == sat:
    m = s.model()
    k = k + 1
    sol = [ m.evaluate(X[i]) for i in range(n)]
    res = res + [(k,sol)]
    forbid = Or([X[i] != sol[i] for i in range(n) ])
    s.add(forbid)     
print(res)

Here we use and, or and != to model our Xforbid constraint. We could have used the same binary variable approach as done in the integer programming model. I tested that also: it turned out to be slower than using integers directly.

Performance

Here are some timings for generating these 48 solutions for the above example:

Model/Solver	Statistics	Solution Time
Binary formulation with Cplex (solution pool)	494 rows 78 binary variables 51092 simplex iterations 3721 nodes	1.6 seconds
Integer formulation with Z3	26 integer variables 693 boolean variables (first model) 5158 clauses (first model) 871 boolean variables (last model) 13990 clauses (last model)	5.5 seconds
Binary formulation with Z3	78 binary variables 860 boolean variables (first model) 2974 clauses (first model) 1015 boolean variables (last model) 6703 clauses (last model)	137 seconds

The binary MIP formulation is not doing poorly at all when solved with a state-of-the-art MIP solver. Z3 really does not like the same binary formulation: we need to use the integer formulation instead to get good performance. Different formulations of the same problem can make a substantial difference in performance.

Van der Waerden (1903-1996)

References

1. Donald E. Knuth, The Art of Computer Programming, Volume 4, Fascicle 6, Satisfiability, 2015
2. Van der Waerden Number, https://en.wikipedia.org/wiki/Van_der_Waerden_number