In (1) a "simple problem" is stated (problems are rarely as simple as they seem):
For the next 18 weeks there is some data about demand for staffing resources:
Actually we don’t need the data for the individual projects: just the totals. It is noted that the maximum number of “bodies” we need is 52 (in week 3).
We start with 48 temps available in the first period. We can let a temp staffer go and we can hire new ones. However when hiring a staffer it will cost 10 days (2 weeks) to train this person. During training a staffer is not productive. We can also keep a staffer idling for a few periods.
To make a difference between idling and training, as shown here:
I will assume that hiring + training is slightly more expensive than keeping someone idle. I think it makes sense to assign some cost to the hiring and training process. This property was not in the original post but I think I have convinced myself that this is actually a reasonable assumption.
To model this I introduce two sets of binary variables:
\[\begin{align} |
We can link \(h_{i,t}\) and \(r_{i,t}\) as follows:
| \[h_{i,t}\ge r_{i,t}-r_{i,t-1}\] |
This implements the implication:
| \[r_{i,t-1}=0 \text{ and } r_{i,t}=1 \implies h_{i,t}=1\] |
that is: if we change \(r\) from 0 to 1, we have a new hire. We will add a (small) cost to a hire to the objective so we don’t need to add constraint to enforce the other way around:
| \[ r_{i,t-1}=1 \text{ or } r_{i,t}=0 \implies h_{i,t}=0\] |
There is one wrinkle here: we need to make sure that the 48 staffers already hired before can work in the first period without being considered to be hired. We can explicitly model this:
| \[h_{i,t}\ge \begin{cases} r_{i,t}-r_{i,t-1} &\text{if $t>1$}\\ r_{i,t}&\text{if $t=1$ and $i>48$}\end{cases}\] |
Actually in the GAMS model below I approached this slightly differently, but with the same net result.
The main equation in the model is to make sure we have enough staffing in each period \(t\). This can be modeled as:
| \[\sum_i \left( r_{i,t} – h_{i,t} - h_{i,t-1}\right) \ge \mathit{demand}_t \] |
The complete model can look like:
Notes:
- \(\mathit{rinit}_{i,t}\) is used to indicate initial staffing when we start period 1. It is sparse: it assumes the value 1 only if \(i=1\) and \(t \le 48\).
- This allows us to write equation EHire as one single, clean equation.
- Note that GAMS will assume a variable is zero outside its domain: \(r_{i,t-1}\) is zero when \(t=1\).
- I used the maximum demand (52 in week 3) to dimension the the problem: set \(i\) has 52 members.
- The model does not decide which workers are idle. We can see in each period how many workers we have and how many are in training. The remaining ones are working or sitting idle.
- We reuse resource numbers \(i\). In the results below worker \(i=21\) is likely to be two different persons.
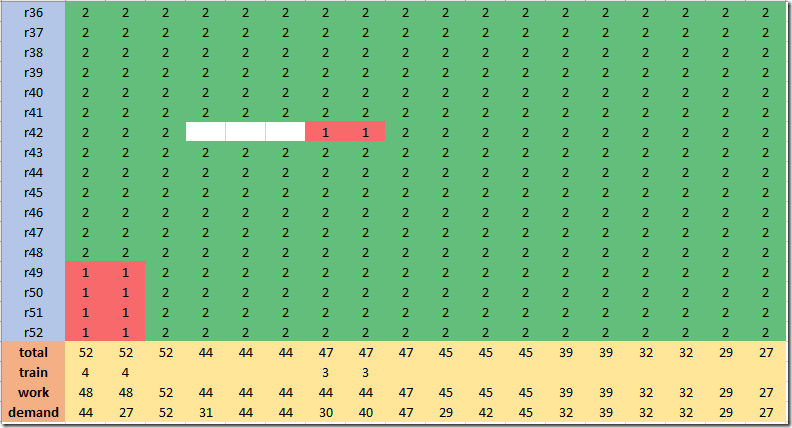
The results look like:
Here a green cell with code=2 means hired and working (or idle, but not in training). A red cell with code=1 means in training. The row “total” is the number of staffers (either working, idling or training). The row “Work” indicates the number of workers available (not in training). We are overshooting demand a bit: some workers are idling.
A picture is always a good idea, so here we see demand vs. staffing available for work.
We see two place where we increase the workforce: we hire in week 1 to handle demand in week 3, and we hire again in week 7 to deal with demand in week 9.
References
- Resources Management Linear Programming, https://stackoverflow.com/questions/44402163/resources-management-linear-programming





No comments:
Post a Comment