Reformulation of non-differentiable term

In a non-linear programming model with a rather complicated objective I see a term

$$\frac{p}{2}\left(|x| + x\right)$$

that is minimized. It is also noted that $p>0$.

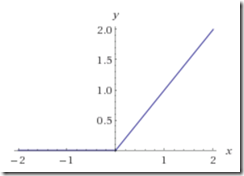
From a picture of $y=\displaystyle\frac{|x|+x}{2}$ we can see this is just a more complicated way of writing:

$$p \max\{0,x\}$$

I don’t see much advantage in using the first form. Both these expressions are non-differentiable at $x=0$. Almost always a better formulation is to replace $\max\{0,x\}$ by a new positive variable $y\ge 0$, and add a constraint:

$$y \ge x$$

Although we are making the model slightly larger (we add a variable and an equation) in general this is good trade-off: we now have a simpler, even linear term in the objective.