Gurobi 6 Distributed vs Concurrent MIP

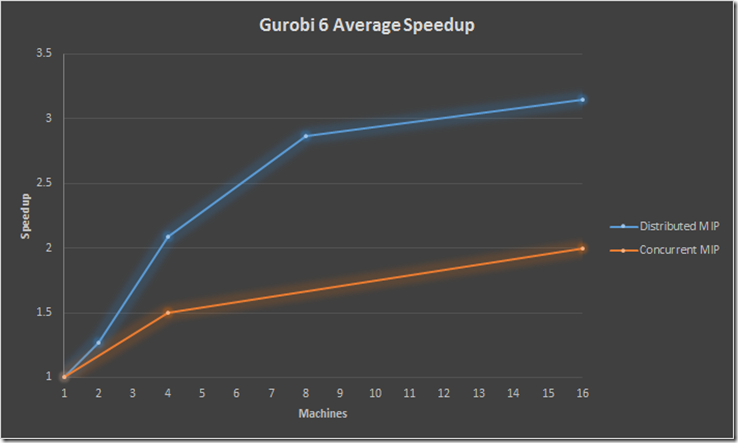
The new Gurobi 6 has quite an attractive offering for running distributed MIPs. Here is a summary for their results (MIPLIB models taking more than 100s).

The concurrent MIP method is just running the same model on different machines with a different random number seed. This changes the solution path sufficiently to actually form a feasible parallel approach. The solution time is the time of the winner. This method always amazes me, but also makes me feel somewhat uncomfortable (the scary question is: if this scheme works does the MIP solver really know what it is doing? – My answer often depends on whether the last MIP I tried was solved ok.). See e.g.: http://coral.ie.lehigh.edu/~jeff/mip-2008/talks/danna.pdf

The distributed MIP is really a distributed MIP where each machine works on parts of the tree. Happy to see this actually works a bit better. Before you buy a ton of machines note that performance starts to tail off after using more than 8 machines. Some numbers showed that a bunch of smaller machines may show better performance than a huge multi-core machine (these SMP machine suffer from memory contention, probably exacerbated by MIP solvers jumping around in memory i.e. suffering from limited locality which hampers exploiting even large caches). Typically several small machines is cheaper than one big one.

Note that every machine in the above picture is actually equipped with a 4 core CPU, so we already have significant parallelism on each machine.

Some other new features:

• Some support for piecewise linear functions. In the objective only and convex only so for a limited class of models for now. Non-convex functions are translated into a MIP formulation.
• General improvements in performance
• Enhancements in lazy constraints