Problems reproducing results

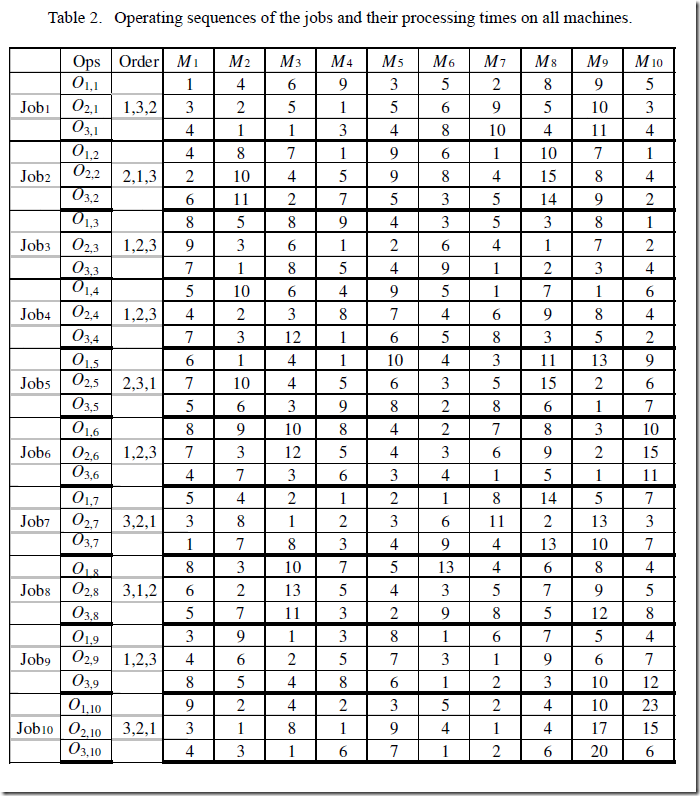
In quite a few cases I have been unable to reproduce published results. Here is an example. (Update: actually the presented results are correct, just a typo in the problem description: see the comments). In the paper http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.138.5011 an example is given of a job shop problem. The data is as follows:

I.e. there are 10 jobs each having 3 job steps. The job steps have to be executed in a certain given order (it might have been easier just to reorder the job step numbers and say all job steps have to be executed in the given order). The authors mention the following:

However when I try to reproduce this with a MIP model I can achieve a makespan of 7. Below is the GAMS model:

$ontext    We try to reproduce the results from    KHALED MESGHOUNI, SLIM HAMMADI, PIERRE BORNE    EVOLUTIONARY ALGORITHMS FOR JOB-SHOP SCHEDULING    Int. J. Appl. Math. Comput. Sci., 2004, Vol. 14, No. 1, 91–103    erwin@amsterdamoptimization.com $offtext sets    j  'jobs' /j1*j10/    m  'machines' /m1*m10/    op 'operations' /op1*op3/    js 'job steps' /js1*js30/ ; table ordering(j,op)     Op1 Op2 Op3 J1   1   3   2 J2   2   1   3 J3   1   2   3 J4   1   2   3 J5   2   3   1 J6   1   2   3 J7   3   2   1 J8   3   1   2 J9   1   2   3 J10  3   2   1 ; table proctime(j,op,m) 'processing times'         M1    M2    M3    M4    M5    M6    M7    M8    M9   M10 J1.Op1   1     4     6     9     3     5     2     8     9     5 J1.Op2   3     2     5     1     5     6     9     5    10     3 J1.Op3   4     1     1     3     4     8    10     4    11     4 J2.Op1   4     8     7     1     9     6     1    10     7     1 J2.Op2   2    10     4     5     9     8     4    15     8     4 J2.Op3   6    11     2     7     5     3     5    14     9     2 J3.Op1   8     5     8     9     4     3     5     3     8     1 J3.Op2   9     3     6     1     2     6     4     1     7     2 J3.Op3   7     1     8     5     4     9     1     2     3     4 J4.Op1   5    10     6     4     9     5     1     7     1     6 J4.Op2   4     2     3     8     7     4     6     9     8     4 J4.Op3   7     3    12     1     6     5     8     3     5     2 J5.Op1   6     1     4     1    10     4     3    11    13     9 J5.Op2   7    10     4     5     6     3     5    15     2     6 J5.Op3   5     6     3     9     8     2     8     6     1     7 J6.Op1   8     9    10     8     4     2     7     8     3    10 J6.Op2   7     3    12     5     4     3     6     9     2    15 J6.Op3   4     7     3     6     3     4     1     5     1    11 J7.Op1   5     4     2     1     2     1     8    14     5     7 J7.Op2   3     8     1     2     3     6    11     2    13     3 J7.Op3   1     7     8     3     4     9     4    13    10     7 J8.Op1   8     3    10     7     5    13     4     6     8     4 J8.Op2   6     2    13     5     4     3     5     7     9     5 J8.Op3   5     7    11     3     2     9     8     5    12     8 J9.Op1   3     9     1     3     8     1     6     7     5     4 J9.Op2   4     6     2     5     7     3     1     9     6     7 J9.Op3   8     5     4     8     6     1     2     3    10    12 J10.Op1  9     2     4     2     3     5     2     4    10    23 J10.Op2  3     1     8     1     9     4     1     4    17    15 J10.Op3  4     3     1     6     7     1     2     6    20     6 ; * * set up a mapping between the job steps (js) and the job/operations (j,o) * sets    jsmap(js,j,op) 'job step mapping between js and (j,o)'    jscur(js) 'temp' /js1/ ; loop((j,op),   jsmap(jscur,j,op)=yes;   jscur(js)=jscur(js-1); ); display jsmap; * * convert data to jobsteps * parameter proctime2(js,m) 'processing time'; proctime2(js,m) = sum(jsmap(js,j,op),proctime(j,op,m)); display proctime2; alias(op,op2),(js,js2),(j,j2); set prec1(j,op,op2) 'ordering as precedence relations'; scalar s; for(s=1 to card(op)-1,    prec1(j,op,op2)$(ordering(j,op)=s and ordering(j,op2)=s+1)=yes; ); display prec1; set prec2(js,js2) 'ordering in terms of job steps'; prec2(js,js2) = sum((j,op,op2)$(jsmap(js,j,op) and jsmap(js2,j,op2)                   and prec1(j,op,op2)),1); display prec2; variables   start(js)           'start time of task'   finish(js)          'completion time'   assign(js,m)        'assign job step to machine'   overlap(js,js2,m)   'binary variable to implement non-overlap'   z                   'objective variable' ; binary variable overlap,assign; positive variable start,finish; scalar TMAX 'max time horizon'; TMAX = sum(js,smin(m,proctime2(js,m))); equations    onemach(js)    calcend    NoOverlap1(js,js2,m)   'machine occupation'    NoOverlap2(js,js2,m)   'machine occupation'    Precedence(js,js2)  'orders need to follow a certain sequence of steps'    zmax(js)           'make span' ; OneMach(js).. sum(m, assign(js,m)) =e= 1; calcEnd(js).. finish(js) =e= start(js) + sum(m, assign(js,m)*proctime2(js,m)); Precedence(prec2(js,js2)).. start(js2) =g= finish(js); set ut(js,js2) 'upper triangular part'; ut(js,js2)$(ord(js)<ord(js2))=yes; NoOverlap1(ut(js,js2),m)..    start(js) =g= finish(js2) - TMAX*overlap(js,js2,m) - TMAX*(1-assign(js,m)) -TMAX*(1-assign(js2,m)); NoOverlap2(ut(js,js2),m)..    start(js2) =g= finish(js)  - TMAX*(1-overlap(js,js2,m))- TMAX*(1-assign(js,m)) -TMAX*(1-assign(js2,m)); zmax(js).. z =G= finish(js); option optcr=0; model jobshop /all/; solve jobshop minimizing z using mip; display start.l,finish.l,assign.l; parameters    start2(j,op)    finish2(j,op)    assign2(j,op,m) ; start2(j,op) = sum(jsmap(js,j,op),start.l(js)); finish2(j,op) = sum(jsmap(js,j,op),finish.l(js)); assign2(j,op,m) = sum(jsmap(js,j,op),assign.l(js,m)); display start2,finish2,assign2; parameter results(j,op,*); results(j,op,'start') = start2(j,op); results(j,op,'proc') = sum(m,assign2(j,op,m)*proctime(j,op,m)); results(j,op,'finish') = finish2(j,op); results(j,op,'machine') = sum(m,assign2(j,op,m)*ord(m)); option results:0; display results;

The model has a few interesting wrinkles:

• I remap the job steps from tuples (job1,op1),(job1,op2),.. to a one dimensional set js1,js2,… This causes some headaches when converting the input data but makes the model equations simpler.
• I map the solution back to the tuples (job1,op1),(job1,op2),.. after the solve.
• A problem with these models is always to find a good big-M. For real problems you may find one by preceding the MIP model with a simple heuristic that constructs an initial solution.
• I try to make sure we don’t compare the job steps twice for overlap if they are scheduled on the same machine. Hence the set UT.

Here are my results:

----    157 PARAMETER results                start        proc      finish     machine j1 .op1           1           1           2           1 j1 .op2           6           1           7           4 j1 .op3           2           1           3           2 j2 .op1           4           1           5           4 j2 .op2           2           2           4           1 j2 .op3           5           2           7           3 j3 .op1                       1           1          10 j3 .op2           3           1           4           4 j3 .op3           6           1           7           7 j4 .op1                       1           1           7 j4 .op2           1           3           4           3 j4 .op3           4           2           6          10 j5 .op1           2           1           3           4 j5 .op2           4           2           6           9 j5 .op3                       1           1           9 j6 .op1                       2           2           6 j6 .op2           2           2           4           9 j6 .op3           4           1           5           7 j7 .op1           5           1           6           4 j7 .op2           1           2           3           8 j7 .op3                       1           1           1 j8 .op1           4           3           7           2 j8 .op2                       2           2           2 j8 .op3           2           2           4           5 j9 .op1           4           1           5           3 j9 .op2           5           1           6           7 j9 .op3           6           1           7           6 j10.op1           4           3           7           5 j10.op2           1           1           2           4 j10.op3                       1           1           3

 

Of course it is possible there is a transcription error in the data table, or may be I am misreading the model, or some other trivial problem. However the results look reasonable when looking at the GANTT charts, i.e. there is no overlap, and the selected machines for processing the job steps are efficient in doing so (we did not select slow machines).

This is actually a fairly small problem and a good MIP code has no problem with it. For instance Gurobi says:

Explored 0 nodes (287 simplex iterations) in 0.47 seconds

I would expect that genetic algorithms become more interesting for larger instances where a MIP solver may not get anywhere.