Time-indexed scheduling model

In the model I am working on we use a time indexed binary variable to model the schedule:

variables    makespan    x(j,t) '=1 if job j starts in period t'    s(j) 'start of job'    z    'elastic infeasibility' ; binary variable x(j,t); positive variable z;

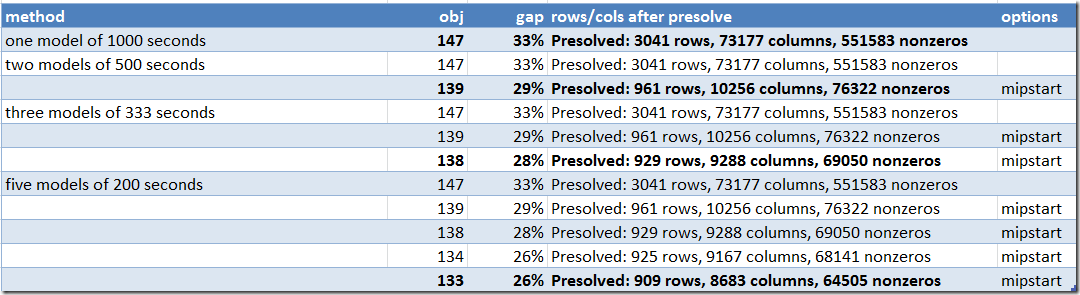
When I solved this model for 1000 seconds, I observed that most of the action takes place in the first few nodes. I was thinking that the following simple algorithm may work to get better improvements:

1. Solve for a shorter time with initial planning horizon giving us a makespan<horizon.
2. Reduce planning horizon to the makespan, and resolve. This model is now smaller, and with MIPSTART we can quickly branch towards the last found solution.
3. Repeat step 2 until out of time.

The loop looks like:

dt.optfile=1; dt.reslim=200; set iter/iter1*iter5/; loop(iter,   solve dt minimizing makespan using mip;   x.fx(j,t)$(tval(t)+duration(j)>makespan.l)=0;   z.fx$(z.l<0.01) = 0;   dt.optfile=2; );

This looks like a reasonable approach:

At least for this case it is better to solve 5 models for 200 seconds than one model for 1,000 seconds. Notice that we reduce the size of the problem in each cycle.