In a multi-objective MIP model I am working I have a binary variable x(t). This variable is mostly zero but now and then it is one. One of the goals is to achieve an even spread of the ones. I.e.
The first row has the ones clustered in the middle. The second one looks pretty good.
The following idea is based on how Q-Q plots are used to find distributions in statistical data (http://en.wikipedia.org/wiki/Q-Q_plot).
First we form a running sum:
The “predicted’ running sum for an evenly distributed x(t) can be expressed as tn/T where n is the total number of ones, t is the current index and T is the last t:
Now we try to keep the values s(t) as close as possible to the predicted values tn/T. I.e.:
Note that n is a variable in my model: I don’t know in advance how many x(t)’s are turned on. Indeed when I run this (with n=3) I see:
| ---- 42 VARIABLE x.L t3 1.000, t7 1.000, t10 1.000 |
Here are the results when we compare the two solutions (click to enlarge):
Indeed this seems to confirm this approach could work, and we can add d(max)-d(min) as an extra objective to minimize.



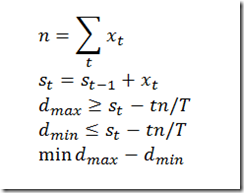

Dear Erwin,
ReplyDeleteA very nice solution indeed. Especially since this solution works in case you do not know the number of ones in advance.
I noticed that shifting all ones a single position to the left, leads to the same "irregularity penalty". Is this what happens for any shift, iow Is your solution "translation invariant"?
Adriaan Hoogendoorn
It almost looks like that. We can subtract or add a constant from dmin and dmax without affecting the difference. Let's see if this can be fixed.
ReplyDeleteI probably should have added dmax ≥ 0, dmin ≤ 0. That will limit how far you can move the pattern around. (Think of dmax,dmin forming a "band-width"; with this constraint the predicted values are inside the band.)
I guess the beauty of this method lies in the fact that you can use whatever distribution. In this case a uniform distribution, which is translation invariant, or a triangular distribution, giving focus to the start or the end of the period, or any other distribution.
ReplyDeleteMaarten Schuerhoff
Hi
ReplyDeleteI have a problem that is similar in spirit to this one. It involves maintaining a distribution of decision variable outcomes in a MP model. That is, I wish the standard deviation of milk production from goats to be equal to a given number, where milk production is determined endogenously. Are you familiar of any way to do this?
Regards
Saul
Without knowing more about the model it is not very wise to give advice. Many formulation issues are heavily dependent on the situation. So the best answer is "It depends".
ReplyDelete