A prototype model was sent to me that was basically a job-shop model. It was formulated with a time index. Unfortunately this model had a large number of time periods, and thus a large model resulted:
* Rows: 4942
* Columns: 10210 (10210 integer, 10210 binary)
* Non-zeros: 137091
The number of time periods needed was estimated as T = sum of processing times. This number is obviously a somewhat generous upper bound and as a result we have a large number of binary variables x[jobstep,timeperiod]. Running some heuristic before solving the MIP can help reducing the estimate for T.
Furthermore, this formulation contained quite a few equations of the form 0 >= 0. The reason was that a particular way was chosen to turn off certain equations:
eq{i in I}: p[i]*(…) >= 0;
where p is a parameter with 0,1 values. Although the LP/MIP pre-solver can take care of these, it is better not to generate those equations at all. I.e. use:
eq{i in I: p[i]=1}: … >= 0;
Even after the presolver removes a lot of rows and columns, the remaining MIP is still quite large:
presolved MIP has 3302 rows, 7339 columns, 124084 non-zeros
7339 integer columns, all of which are binary
With a continuous time formulation (no time index) and better care of generating only equations that are really needed, a much smaller model can be formed:
* Rows: 150
* Columns: 91 (36 integer, 36 binary)
* Non-zeros: 371
In this model T is no longer used to determine the number of variables. However it is used to form some big-M values which are present in “job step i is executed before or after job step j” (i.e. no overlap) constraints.
Large scale example:
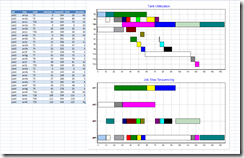


Perhaps we need a term for this, say NP_L (a model is nonpolynomially larded if the size of the model grows faster than any polynomial function of the size of what is actually needed)?
ReplyDeletemay i know,how to solve jssp using genetic algorithm in matlab?
ReplyDelete