This is a follow up on http://yetanothermathprogrammingconsultant.blogspot.com/2010/03/looks-difficult-to-me.html
I tried a simple minded MINLP formulation, and solved this with Baron:
This actually worked! Even for n=100 and n=200. Note that it is important to use a global solver as there are many inferior local solutions. As I solved with OPTCR=0 these are really proven global optimal solutions. I assumed the rectangle can not be rotated and must be aligned with the x and y axes. Here are some results.
Here are the corresponding plots of the solutions:
Of course faster special purpose algorithms exist for this problem.



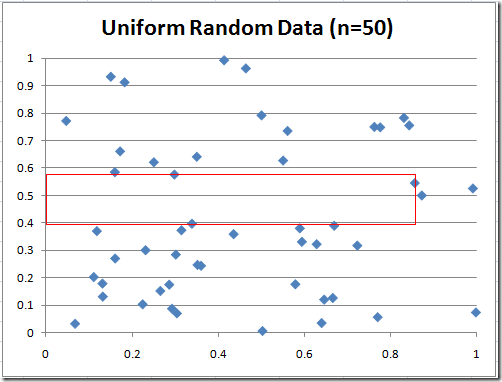


800 seconds for 200 points seem a lot. There are relatively few locally maximal rectangles. They are bounded by points from all four sides.
ReplyDeleteWe can just take any combination of two points, they would be on the left and right edges of the rectangle. If there's a point in the rectangle defined by those two points as corners, we move on, otherwise we extend the top and bottom as much as we can. This algorithm would be cubic in the number of points and is basically an exhaustive search. Some smarts can improve it, as for most pairs of points, there will already be a point inbetween.
Seems too good to be true, am I missing something?
Baron is a global solver. That are by nature not as fast as local solvers. Yes, I believe there are O(n^2) algorithms and even faster ones to do this. I was just curious if this could be solved by stating it as a math programming problem.
ReplyDelete