In the paper
Hybrid Approach for Machine Scheduling Optimization in Custom Furniture Industry
Juan C. Vidal, Manuel Mucientes, Alberto Bugarin, and Manuel Lama
Department of Electronics and Computer Science
University of Santiago de Compostela, E-15782 Spain
http://www.gsi.dec.usc.es/printable/node/793
a data set is used, which I recognized from http://yetanothermathprogrammingconsultant.blogspot.com/2012/08/problems-reproducing-results.html. It is just a bit smaller:
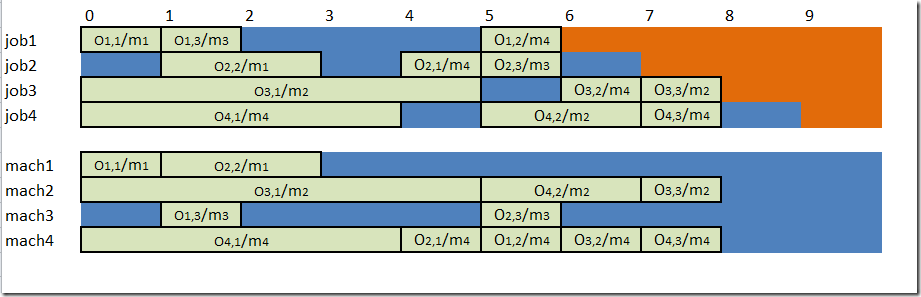
The main addition is the addition of due dates. The idea is to develop a bi-criteria model that minimizes the makespan and the total tardiness. Unfortunately when we just minimize the makespan, we get a solution with all jobs being finished on-time:
---- 179 PARAMETER results
start proc finish machine due
j1 .op1 1 1 1
j1 .op2 5 1 6 4 6
j1 .op3 1 1 2 3
j2 .op1 4 1 5 4
j2 .op2 1 2 3 1
j2 .op3 5 2 7 3 7
j3 .op1 5 5 2
j3 .op2 6 1 7 4
j3 .op3 7 1 8 2 8
j4 .op1 4 4 4
j4 .op2 5 2 7 2
j4 .op3 7 1 8 4 9
makespan. 8
I.e. for this data we just can minimize the makespan and we are done. This is really boring. It would be better to have a data set that really needs to explore an efficient frontier. I tried with some different due dates e.g.
parameter duedate(j) /
J1 3
J2 9
J3 9
J4 9
/;
but that still makes the problem too easy (just two efficient points easily found by solving for each of the objectives).
I am working (in another context) on some MIP formulations for these type of problems. Hence my interest. Ok, we’ll keep looking for better examples…
Update: I changed the data a bit (added two more jobs). Now at least I get three efficient solutions:
The smooth line connecting the efficient points is for beautification: the line does not really form the efficient frontier. This is because the problem is discrete.


No comments:
Post a Comment