Cplex QP problems

For a reasonable sized continuous QP problem, the default Cplex settings indicate problems:

Reading data... Starting Cplex... Tried aggregator 1 time. QP Presolve eliminated 51 rows and 60 columns. Aggregator did 600 substitutions. Reduced QP has 1404 rows, 25401 columns, and 58593 nonzeros. Reduced QP objective Q matrix has 24979 nonzeros. Presolve time =    0.03 sec. Parallel mode: none, using 1 thread for barrier Number of nonzeros in lower triangle of A*A' = 23873 Using Approximate Minimum Degree ordering Total time for automatic ordering = 0.00 sec. Summary statistics for Cholesky factor:   Rows in Factor            = 1404   Integer space required    = 12305   Total non-zeros in factor = 37816   Total FP ops to factor    = 1398232 Itn      Primal Obj        Dual Obj  Prim Inf Upper Inf  Dual Inf             0  1.1269359e+016 -1.1269360e+016 1.03e+006 0.00e+000 6.83e+014    1  1.3889591e+015 -1.3889592e+015 3.62e+005 0.00e+000 2.40e+014    2  5.4393422e+013 -5.4393451e+013 7.16e+004 0.00e+000 4.75e+013    3  4.9247681e+011 -4.9248040e+011 6.82e+003 0.00e+000 4.51e+012    4  2.8122639e+009 -2.8128116e+009 5.15e+002 0.00e+000 3.41e+011    5  1.2862048e+008 -1.2878713e+008 1.10e+002 0.00e+000 7.29e+010    6  1.6614552e+006 -1.6932044e+006 1.25e+001 0.00e+000 8.26e+009    7  3.0507032e+003 -9.1387053e+003 1.16e-001 0.00e+000 7.70e+007    8  8.8731205e+002 -2.6509477e+003 3.31e-002 0.00e+000 2.19e+007    9  3.2742736e+002 -5.8146949e+002 8.03e-003 0.00e+000 5.32e+006   10  2.4615010e+002 -2.3471413e+002 4.40e-003 0.00e+000 2.92e+006   11  2.0803982e+002 -3.1756372e+001 2.26e-003 0.00e+000 1.50e+006   12  1.8984146e+002  9.9701542e+001 8.66e-004 0.00e+000 5.74e+005   13  1.8441405e+002  1.5886308e+002 2.46e-004 0.00e+000 1.63e+005   14  1.8341125e+002  1.7590746e+002 7.24e-005 0.00e+000 4.80e+004   15  1.8320505e+002  1.8209849e+002 1.04e-005 0.00e+000 6.88e+003   16  1.8318478e+002  1.8309471e+002 7.96e-007 0.00e+000 5.27e+002   17  1.8318341e+002  1.8318113e+002 1.57e-008 0.00e+000 1.04e+001   18  1.8318336e+002  1.8318333e+002 1.14e-010 0.00e+000 7.37e-002   19  1.8318506e+002  1.8317840e+002 3.79e-011 0.00e+000 3.91e-004   20  1.8318506e+002  1.8317840e+002 3.12e-007 0.00e+000 3.44e+004   *   1.8318506e+002  1.8317840e+002 3.79e-011 0.00e+000 3.91e-004 Total time on 1 threads =    0.19 sec. QP status(6): non-optimal Solution available but not proven optimal due to numerical difficulties.

This is a matrix balancing problem, where we try to repair economic data matrices after dropping small values, while maintaining some important economic identities.

First thing I tried was to use primal and dual simplex methods, but these turned out not very attractive alternatives (primal simplex took a long time, and dual simplex was infeasible after unscaling). The best option turned out to be using the opfion  numericalemphasis. Now it solves fine. Of course I believe that I should not have to do this: Cplex itself should understand better than me that it is in trouble and should try to recover from this in a more intelligent way than I can.

Not such a good example data set

In the paper

Hybrid Approach for Machine Scheduling Optimization in Custom Furniture Industry
Juan C. Vidal, Manuel Mucientes, Alberto Bugarin, and Manuel Lama
Department of Electronics and Computer Science
University of Santiago de Compostela, E-15782 Spain
http://www.gsi.dec.usc.es/printable/node/793

a data set is used, which I recognized from http://yetanothermathprogrammingconsultant.blogspot.com/2012/08/problems-reproducing-results.html. It is just a bit smaller:

The main addition is the addition of due dates. The idea is to develop a bi-criteria model that minimizes the makespan and the total tardiness. Unfortunately when we just minimize the makespan, we get a solution with all jobs being finished on-time:

----    179 PARAMETER results 

                   start        proc      finish     machine         due

j1      .op1                       1           1           1
j1      .op2           5           1           6           4           6
j1      .op3           1           1           2           3
j2      .op1           4           1           5           4
j2      .op2           1           2           3           1
j2      .op3           5           2           7           3           7
j3      .op1                       5           5           2
j3      .op2           6           1           7           4
j3      .op3           7           1           8           2           8
j4      .op1                       4           4           4
j4      .op2           5           2           7           2
j4      .op3           7           1           8           4           9
makespan.                                      8

I.e. for this data we just can minimize the makespan and we are done. This is really boring. It would be better to have a data set that really needs to explore an efficient frontier. I tried with some different due dates e.g.

parameter duedate(j) /
  J1 3
  J2 9
  J3 9
  J4 9
/;

but that still makes the problem too easy (just two efficient points easily found by solving for each of the objectives).

I am working (in another context) on some MIP formulations for these type of problems. Hence my interest. Ok, we’ll keep looking for better examples…

 

Update: I changed the data a bit (added two more jobs). Now at least I get three efficient solutions:

The smooth line connecting the efficient points is for beautification: the line does not really form the efficient frontier. This is because the problem is discrete.  

The Comparative Productivity of Programming Languages

http://www.drdobbs.com/jvm/the-comparative-productivity-of-programm/240005881

I would have expected programmers to be about as efficient in C# as in Java. Of course it is possible the underlying statistical model is not correct for making a statement like this. E.g. in the sample there were many seasoned Java programmers but on the other hand many relative junior C# programmers. If so, was this taken care of in the regression?

Surprises in the log file

Sometimes I see messages in the log file of a MIP solver that are quite worrying. Here is one from GAMS/Cplex:

Proven optimal solution. MIP Solution:           15.353413    (10612 iterations, 238 nodes) Final Solve:            17.208664    (82 iterations)

The final solve is a extra LP GAMS wants to solve after fixing all integer variables (the reason is they want to report marginals i.e. duals and reduced cost). Obviously the two objectives should be (almost) the same. Here we see a large difference, indicating we are probably in deep trouble.

Problems reproducing results

In quite a few cases I have been unable to reproduce published results. Here is an example. (Update: actually the presented results are correct, just a typo in the problem description: see the comments). In the paper http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.138.5011 an example is given of a job shop problem. The data is as follows:

I.e. there are 10 jobs each having 3 job steps. The job steps have to be executed in a certain given order (it might have been easier just to reorder the job step numbers and say all job steps have to be executed in the given order). The authors mention the following:

However when I try to reproduce this with a MIP model I can achieve a makespan of 7. Below is the GAMS model:

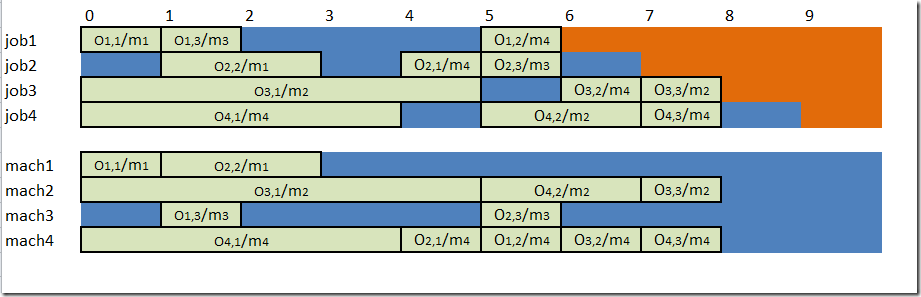
$ontext    We try to reproduce the results from    KHALED MESGHOUNI, SLIM HAMMADI, PIERRE BORNE    EVOLUTIONARY ALGORITHMS FOR JOB-SHOP SCHEDULING    Int. J. Appl. Math. Comput. Sci., 2004, Vol. 14, No. 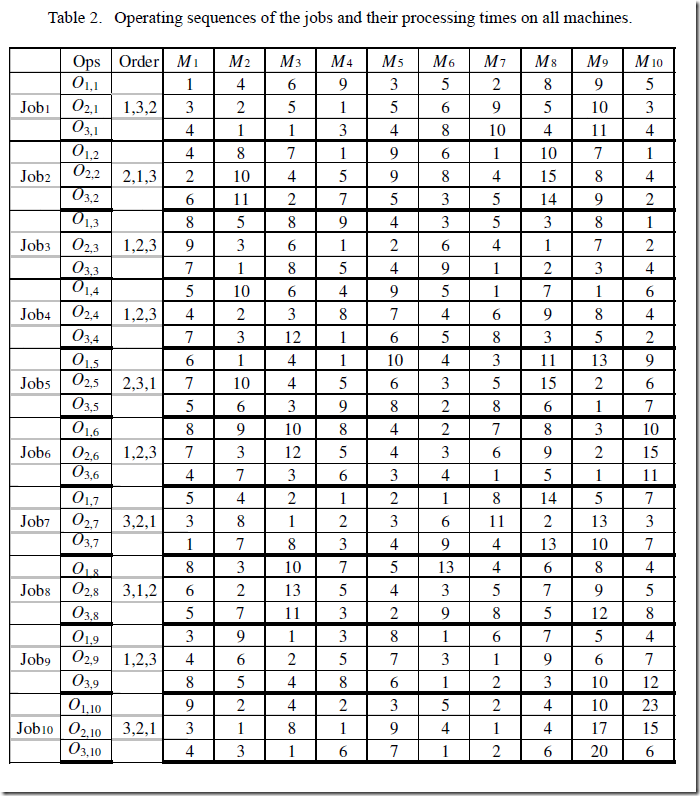1, 91–103    erwin@amsterdamoptimization.com $offtext sets    j  'jobs' /j1*j10/    m  'machines' /m1*m10/    op 'operations' /op1*op3/    js 'job steps' /js1*js30/ ; table ordering(j,op)     Op1 Op2 Op3 J1   1   3   2 J2   2   1   3 J3   1   2   3 J4   1   2   3 J5   2   3   1 J6   1   2   3 J7   3   2   1 J8   3   1   2 J9   1   2   3 J10  3   2   1 ; table proctime(j,op,m) 'processing times'         M1    M2    M3    M4    M5    M6    M7    M8    M9   M10 J1.Op1   1     4     6     9     3     5     2     8     9     5 J1.Op2   3     2     5     1     5     6     9     5    10     3 J1.Op3   4     1     1     3     4     8    10     4    11     4 J2.Op1   4     8     7     1     9     6     1    10     7     1 J2.Op2   2    10     4     5     9     8     4    15     8     4 J2.Op3   6    11     2     7     5     3     5    14     9     2 J3.Op1   8     5     8     9     4     3     5     3     8     1 J3.Op2   9     3     6     1     2     6     4     1     7     2 J3.Op3   7     1     8     5     4     9     1     2     3     4 J4.Op1   5    10     6     4     9     5     1     7     1     6 J4.Op2   4     2     3     8     7     4     6     9     8     4 J4.Op3   7     3    12     1     6     5     8     3     5     2 J5.Op1   6     1     4     1    10     4     3    11    13     9 J5.Op2   7    10     4     5     6     3     5    15     2     6 J5.Op3   5     6     3     9     8     2     8     6     1     7 J6.Op1   8     9    10     8     4     2     7     8     3    10 J6.Op2   7     3    12     5     4     3     6     9     2    15 J6.Op3   4     7     3     6     3     4     1     5     1    11 J7.Op1   5     4     2     1     2     1     8    14     5     7 J7.Op2   3     8     1     2     3     6    11     2    13     3 J7.Op3   1     7     8     3     4     9     4    13    10     7 J8.Op1   8     3    10     7     5    13     4     6     8     4 J8.Op2   6     2    13     5     4     3     5     7     9     5 J8.Op3   5     7    11     3     2     9     8     5    12     8 J9.Op1   3     9     1     3     8     1     6     7     5     4 J9.Op2   4     6     2     5     7     3     1     9     6     7 J9.Op3   8     5     4     8     6     1     2     3    10    12 J10.Op1  9     2     4     2     3     5     2     4    10    23 J10.Op2  3     1     8     1     9     4     1     4    17    15 J10.Op3  4     3     1     6     7     1     2     6    20     6 ; * * set up a mapping between the job steps (js) and the job/operations (j,o) * sets    jsmap(js,j,op) 'job step mapping between js and (j,o)'    jscur(js) 'temp' /js1/ ; loop((j,op),   jsmap(jscur,j,op)=yes;   jscur(js)=jscur(js-1); ); display jsmap; * * convert data to jobsteps * parameter proctime2(js,m) 'processing time'; proctime2(js,m) = sum(jsmap(js,j,op),proctime(j,op,m)); display proctime2; alias(op,op2),(js,js2),(j,j2); set prec1(j,op,op2) 'ordering as precedence relations'; scalar s; for(s=1 to card(op)-1,    prec1(j,op,op2)$(ordering(j,op)=s and ordering(j,op2)=s+1)=yes; ); display prec1; set prec2(js,js2) 'ordering in terms of job steps'; prec2(js,js2) = sum((j,op,op2)$(jsmap(js,j,op) and jsmap(js2,j,op2)                   and prec1(j,op,op2)),1); display prec2; variables   start(js)           'start time of task'   finish(js)          'completion time'   assign(js,m)        'assign job step to machine'   overlap(js,js2,m)   'binary variable to implement non-overlap'   z                   'objective variable' ; binary variable overlap,assign; positive variable start,finish; scalar TMAX 'max time horizon'; TMAX = sum(js,smin(m,proctime2(js,m))); equations    onemach(js)    calcend    NoOverlap1(js,js2,m)   'machine occupation'    NoOverlap2(js,js2,m)   'machine occupation'    Precedence(js,js2)  'orders need to follow a certain sequence of steps'    zmax(js)           'make span' ; OneMach(js).. sum(m, assign(js,m)) =e= 1; calcEnd(js).. finish(js) =e= start(js) + sum(m, assign(js,m)*proctime2(js,m)); Precedence(prec2(js,js2)).. start(js2) =g= finish(js); set ut(js,js2) 'upper triangular part'; ut(js,js2)$(ord(js)<ord(js2))=yes; NoOverlap1(ut(js,js2),m)..    start(js) =g= finish(js2) - TMAX*overlap(js,js2,m) - TMAX*(1-assign(js,m)) -TMAX*(1-assign(js2,m)); NoOverlap2(ut(js,js2),m)..    start(js2) =g= finish(js)  - TMAX*(1-overlap(js,js2,m))- TMAX*(1-assign(js,m)) -TMAX*(1-assign(js2,m)); zmax(js).. z =G= finish(js); option optcr=0; model jobshop /all/; solve jobshop minimizing z using mip; display start.l,finish.l,assign.l; parameters    start2(j,op)    finish2(j,op)    assign2(j,op,m) ; start2(j,op) = sum(jsmap(js,j,op),start.l(js)); finish2(j,op) = sum(jsmap(js,j,op),finish.l(js)); assign2(j,op,m) = sum(jsmap(js,j,op),assign.l(js,m)); display start2,finish2,assign2; parameter results(j,op,*); results(j,op,'start') = start2(j,op); results(j,op,'proc') = sum(m,assign2(j,op,m)*proctime(j,op,m)); results(j,op,'finish') = finish2(j,op); results(j,op,'machine') = sum(m,assign2(j,op,m)*ord(m)); option results:0; display results;

The model has a few interesting wrinkles:

• I remap the job steps from tuples (job1,op1),(job1,op2),.. to a one dimensional set js1,js2,… This causes some headaches when converting the input data but makes the model equations simpler.
• I map the solution back to the tuples (job1,op1),(job1,op2),.. after the solve.
• A problem with these models is always to find a good big-M. For real problems you may find one by preceding the MIP model with a simple heuristic that constructs an initial solution.
• I try to make sure we don’t compare the job steps twice for overlap if they are scheduled on the same machine. Hence the set UT.

Here are my results:

----    157 PARAMETER results                start        proc      finish     machine j1 .op1           1           1           2           1 j1 .op2           6           1           7           4 j1 .op3           2           1           3           2 j2 .op1           4           1           5           4 j2 .op2           2           2           4           1 j2 .op3           5           2           7           3 j3 .op1                       1           1          10 j3 .op2           3           1           4           4 j3 .op3           6           1           7           7 j4 .op1                       1           1           7 j4 .op2           1           3           4           3 j4 .op3           4           2           6          10 j5 .op1           2           1           3           4 j5 .op2           4           2           6           9 j5 .op3                       1           1           9 j6 .op1                       2           2           6 j6 .op2           2           2           4           9 j6 .op3           4           1           5           7 j7 .op1           5           1           6           4 j7 .op2           1           2           3           8 j7 .op3                       1           1           1 j8 .op1           4           3           7           2 j8 .op2                       2           2           2 j8 .op3           2           2           4           5 j9 .op1           4           1           5           3 j9 .op2           5           1           6           7 j9 .op3           6           1           7           6 j10.op1           4           3           7           5 j10.op2           1           1           2           4 j10.op3                       1           1           3

 

Of course it is possible there is a transcription error in the data table, or may be I am misreading the model, or some other trivial problem. However the results look reasonable when looking at the GANTT charts, i.e. there is no overlap, and the selected machines for processing the job steps are efficient in doing so (we did not select slow machines).

This is actually a fairly small problem and a good MIP code has no problem with it. For instance Gurobi says:

Explored 0 nodes (287 simplex iterations) in 0.47 seconds

I would expect that genetic algorithms become more interesting for larger instances where a MIP solver may not get anywhere.

Infes and Nopt

GAMS flags rows and columns in the solution by NOPT or INFES if they are non-optimal or infeasible. The NOPT basically signal the marginal of the row or column has the wrong sign. A marginal on a row is simply the dual and a marginal on a column is the reduced cost (this can be interpreted as the dual if the bound was written as a constraint instead).

If the model is infeasible it does not make sense to report NOPTs. In this case we don’t even know about which objective we are talking about (phase I or phase II objective). Hence the following output of GAMS/CPlex is really a bug in the Cplex link:

 

**** REPORT SUMMARY :      115     NONOPT ( NOPT)

                           257 INFEASIBLE (INFES)

---- EQU mula2  linearization of a(p,o)=c(p)*u(o)

                      LOWER     LEVEL     UPPER    MARGINAL

project1 .indirect     -INF       .         .         EPS      

project1 .direct       -INF       .         .       -1.000  NOPT

project1 .tech         -INF       .         .         EPS      

project1 .social       -INF       .         .       -1.000  NOPT

---- EQU mulb2  linearization of b(p,i)=c(p)*v(i)

                  LOWER     LEVEL     UPPER    MARGINAL

project1 .cost     -INF  8.6094E+6      .       -1.000 INFES

project2 .cost     -INF  8.6094E+6      .       -1.000 INFES

project3 .cost     -INF  8.6094E+6      .       -1.000 INFES

Error messages vs format strings

Sometimes we see sloppy handling of error messages where format strings are popping up. Of course those form strings should not be displayed as is, bit should be used to compose a complete error message. Here is an example with GAMS/Cplex:

*** CPLEX Error  5002: Q in %s is not positive semi-definite.

Another example is coming from the Delphi run time, when a file could not be written. This is from an exception generated in this case:

EInOutError: Invalid file name - %s

Javascript: adding array methods

I used a.indexOf(“a”) to find the position of “a” inside an array. Turns out this an extension not supported by Internet Explorer.

But from http://stackoverflow.com/questions/2790001/fixing-javascript-array-functions-in-internet-explorer-indexof-foreach-etc we see how easy it is to add this function in case it is missing.

// Add ECMA262-5 Array methods if not supported natively
//
if (!('indexOf' in Array.prototype)) {
    Array.prototype.indexOf= function(find, i /*opt*/) {
        if (i===undefined) i= 0;
        if (i<0) i+= this.length;
        if (i<0) i= 0;
        for (var n= this.length; i<n; i++)
            if (i in this && this[i]===find)
                return i;
        return -1;
    };
}

Pretty cool. Of course here it helps that Javascript is not type-checked (otherwise one would need generics or something like that).