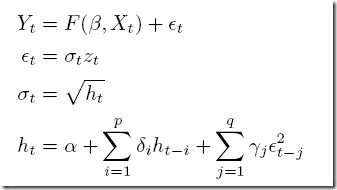For some NLP models defined variables can help to reduce the size of the optimization model while maintaining readability. Defined variables are variables that will be removed by the modeling system by substitution. Sometimes introduction of defined variables in the model requires a little bit of thought. In this example we consider a maximum likelihood estimation problem of a GARCH(p,q) process. GARCH time series are often used in financial applications.
The GARCH(p,q) model can be described as:
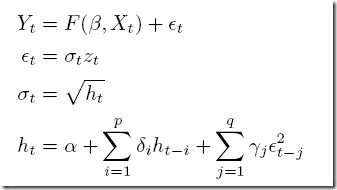 where εt follows a process described by the last three equations and zt has a Gaussian distribution. We assume the simplest functional form for F:
where εt follows a process described by the last three equations and zt has a Gaussian distribution. We assume the simplest functional form for F:
 i.e. a constant value. The parameters to estimate are θ=(μ,α,δi,γj). The optimization problem for finding these can be written as:
i.e. a constant value. The parameters to estimate are θ=(μ,α,δi,γj). The optimization problem for finding these can be written as:
 where we maximize the log likelihood function subject to some stationarity condition. We can simplify the objective to:
where we maximize the log likelihood function subject to some stationarity condition. We can simplify the objective to:

In this document I describe a GAMS implementation. We use extra variables for εt and ht. The basic model looks like:
variables
L 'log likelihood (constants taken out)'
h(t) 'sigma(t)=sqrt(h(t))'
e(t) 'residuals'
alpha_0 'GARCH parameter (constant)'
alpha(q) 'GARCH parameters (q)'
beta(p) 'GARCH parameters (p)'
constant 'information structure: y = constant + e'
;
equations
loglike 'transformed log likelihood function'
def_h(t) 'h(t) structure'
stat_garch 'stationarity condition (GARCH model)'
series(t) 'defines the time series'
;
loglike.. L =e= sum(lag(t), log(h(t)) + sqr(e(t))/h(t) );
def_h(lag(t)).. h(t) =e= alpha_0 + sum(q, alpha(q)*sqr(e(t-ord(q))))
+ sum(p, beta(p)*h(t-ord(p))) ;
stat_garch.. sum(q,alpha(q)) + sum(p,beta(p)) =l= 1;
series(lag(t)).. y(t) =e= constant + e(t);
model garch /loglike, def_h, stat_garch, series/;
solve garch using nlp minimizing L;
Here lag is a subset so we don’t go beyond the border when evaluating lagged variables ht-i and εt-j. Note that we have many more variables in this model than original stated. Especially ht and εt contribute. The model statistics are:
MODEL STATISTICS
BLOCKS OF EQUATIONS 4 SINGLE EQUATIONS 2,084
BLOCKS OF VARIABLES 7 SINGLE VARIABLES 2,089
NON ZERO ELEMENTS 10,413 NON LINEAR N-Z 6,246
DERIVATIVE POOL 2,089 CONSTANT POOL 16
CODE LENGTH 40,602
The results for the GARCH(1,1) case are:
---- 439 VARIABLE L.L = 329.732 log likelihood (constants taken out)
VARIABLE alpha_0.L = 0.019 GARCH parameter (constant)
---- 439 VARIABLE alpha.L GARCH parameters (q)
q1 0.042
---- 439 VARIABLE beta.L GARCH parameters (p)
p1 0.919
Can we reproduce with AMPL using defined variables? Not very difficult. The real problem is how to deal with ht and εt for t ≤ max(p,q)+1. The GAMS model actually lets them float. The εt‘s are small so we can just fix them: it would not make much difference in the solution. Actually I believe in the GAMS model we should have used:
series(t1(t)).. y(t) =e= constant + e(t);
The initial ht‘s are more important. Lets try to mimic the GAMS implementation here. We do that with an additional variable h0. The complete AMPL model looks like:
set T ordered;
param s{T};
set T1 ordered := T diff {first(T)};
param y{t in T1} := 100*log(s[t]/s[prev(t,T)]);
param p = 1;
param q = 1;
param mpq = max(p,q);
# create a set where we drop the first mpq entries from T1
set Lag ordered := {i in T1: ord(i,T1) > mpq};
var constant;
var alpha_0 >= 0.0001, <= 100, := .1;
var alpha{i in 1..q} >= 0, <= 100, := .1;
var beta{j in 1..p} >= 0, <= 100, := .1;
var e{t in T1} = y[t] - constant;
set T0 := T1 diff Lag;
var h0{t in T0} >= 0.0001;
var h{t in T1} =
if (t in Lag) then (alpha_0 + sum{i in 1..q} alpha[i]*e[prev(t,T,i)]^2
+ sum{j in 1..p} beta[j]*h[prev(t,T,j)])
else h0[t];
minimize L: sum{t in Lag} (log(h[t]) + e[t]^2/h[t]);
stat_garch: sum{i in 1..q} alpha[i] + sum{j in 1..p} beta[j] <= 1;
This generates a very small model:
Substitution eliminates 2084 variables.
Adjusted problem:
5 variables, all nonlinear
1 constraint, all linear; 2 nonzeros
1 nonlinear objective; 5 nonzeros.
MINOS 5.5: optimal solution found.
30 iterations, objective 329.731725
Nonlin evals: obj = 85, grad = 84.
ampl: display L,alpha_0,alpha,beta;
L = 329.732
alpha_0 = 0.0194425
: alpha beta :=
1 0.0415491 0.919192
;
This indeed is much smaller than the GAMS model. The exercise was also useful as it revealed some soft spots in the GAMS formulation. I probably need to rethink how we deal with initial ht‘s in the GAMS model: the results are sensitive to how this is handled.